Table of Contents

C++17 brings us parallel algorithms. However, there are not many implementations where you can use the new features. The situation is getting better and better, as we have the MSVC implementation and now Intel’s version will soon be available as the base for libstdc++ for GCC. Since the library is important, I’ve decided to see how to use it and what it offers.

Intro  

Until now on this blog, you could read articles where I experimented only with the MSVC implementation of parallel algorithms from C++17. For example:

However, there’s also another implementation that is worth checking – the one coming with Intel® C++ compiler. I will further refer to it as “Intel’s Parallel STL”. The library is important as it’s the backbone of future, implementations for GCC and possibly Clang/LLVM.

About C++17 Parallel Algorithms  

With Parallel Algorithms added in C++17 you can invoke many algorithms using “execution policies”. So far we have three options:

  • std::execution::seq - sequential execution, implements sequenced_policy type.
  • std::execution::par - parallel execution, implements parallel_policy type.
  • std::execution::par_unseq - parallel and unsequenced execution, implements parallel_unsequenced_policy type.

The vital information is that the execution policies are permissions, not obligations. Each library implementation might choose what can be parallelised and how.

To use parallel algorithms, you need at least forward iterators.

For example:

auto myVec = GenerateVector();
std::vector<...> outVec(myVec.size());
std::copy(std::execution::par, myVec.begin(), myVec.end(), outVec.begin());
       // ^^^^^^^^^^^^^^^^^^^
       // execution policy

The above code uses par policy. However, implementations might decide not to use parallelism. In copy operations we might be memory bound, so using more threads won’t speed up things.

About Intel Parallel STL  

Developers at Intel built the library to show early support for C++17 Parallel Algorithms. Intel offers many computing and threading solutions, and the library leverages Intel’s famous Threading Building Blocks (TBB).

Here’s the best and concise description of the library:

Parallel STL is an implementation of the C++ standard library algorithms with support for execution policies, as specified in ISO/IEC 14882:2017 standard, commonly called C++17. The implementation also supports the unsequenced execution policy specified in Parallelism TS version 2 and proposed for the next version of the C++ standard in the C++ working group paper P1001R1.

Parallel STL offers efficient support for both parallel and vectorised execution of algorithms for Intel® processors. For sequential execution, it relies on an available implementation of the C++ standard library.

The main repository is located at Github: https://github.com/intel/parallelstl
Also, the getting started document: https://software.intel.com/en-us/get-started-with-pstl

The library can work with any C++11 compiler that works with TBB. Also, for vectorisation (unsequenced policies) your compiler should support OpenMP 4.0 SIMD constructs.

To use the library you have to include the following headers:

#include <pstl/algorithm>  // most of the algorithms
#include <pstl/numeric>    // for reduce, transform_reduce
#include <pstl/execution>  // execution policies
#include <pstl/memory>

The library offers four different execution policies:

  • pstl::execution::seq - sequential execution
  • pstl::execution::unseq - unsequenced SIMD execution. This is not supported in C++17, but might be available in C++20 (see P0076).
  • pstl::execution::par - parallel execution
  • pstl::execution::par_unseq - parallel and SIMD

The use of the library is very similar to the Standard library, instead of std::execution::par you just need to use pstl::execution::par.

auto myVec = GenerateVector();
std::std::sort(pstl::execution::par, myVec.begin(), myVec.end());

While C++17 requires Forward Iterators for parallel algorithms, Intel’s library needs stronger condition: Random Access Iterators.

Backbone Implementation For GCC  

The exciting information is that Intel’s implementation serves as a backbone for the upcoming GCC’s (probably GCC 9.0?) version.

Here’s a video from Thomas Rodgers (the developer that brings Intel’s work into GCC)

OpenMP 4.0 is also available under GCC so there’s also a good chance that unsequenced policies will also be available in GCC.

Here’s also a thread for LLVM project:
[cfe-dev] [RFC] C++17 Parallel STL ∥ a new project

How To Install Parallel STL  

The library is header only, so you have to download the files.
However the library depends on TBB, so you also have to install in the system.

You can use the following link:
Download | Threading Building Blocks

New Conan Package  

Thanks to the support from the Conan Team we added Parallel STL as a Conan package.

https://bintray.com/conan-community/conan/parallelstl%3Aconan

To install the library, you can type:

conan install parallelstl/20181004@conan/stable

The command will install TBB along with the headers for Parallel STL in your system.

About Test Code  

For the test code, apart from Parallel STL I also needed glm (OpenGL Math library) and Google Benchmark. Plus of course Visual Studio.

The repo: https://github.com/fenbf/Intel-Parallel-STL-Tests

In my previous benchmarks, I’ve used custom code to measure execution. This time I’ve decided to rely on google benchmark - as it offers more options and should give more consistent results.

To manage all dependencies and libraries, I’m using Conan Package Manager.

Conan file - conanfile.txt:

[requires]
glm/0.9.9.1@g-truc/stable
parallelstl/20181004@conan/stable 
google-benchmark/1.4.1@mpusz/stable

[generators]
visual_studio

Here’s the command line to install the library (it generates *.props file that I can use with my Visual Studio project)

conan install . -s build_type=Release -if build_release_x64 -s arch=x86_64

Note about google benchmark: Currently, the library is not in conan center repository, so I’m using a package created by Mateusz Pusz (read more here: https://github.com/mpusz/conan-google-benchmark). To use it in your system you only have to add a remote URL:

conan remote add conan-mpusz https://api.bintray.com/conan/mpusz/conan-mpusz

As I know, we should also expect to have google benchmark in conan center soon.

I remember that a year or two ago it was a real pain for me to manage the libraries for my small projects, but with Conan, it’s now straightforward.

Tests  

I made the following tests:

  • Trigonometry - sqrt(sin*cos)
  • Dot product using large vectors
  • Sorting of vec4, on the X axis
  • Extra example :)

Trigonometry  

As the first example let’s start with something that can be “easily” parallelisable: computing trigonometry functions. The instructions should keep CPU busy, and since there’s no dependency between element computations, then we can see a nice speed increase.

The code:

template <typename Policy>
static void BM_Trigonometry(benchmark::State& state, Policy execution_policy) 
{
    std::vector<double> vec(state.range(0), 0.5);
    std::generate(vec.begin(), vec.end(), []() { 
        return GenRandomFloat(0.0f, 0.5f*glm::pi<float>()); }
    );
    std::vector out(vec);

    for (auto _ : state)
    {
        std::transform(execution_policy, 
                       vec.begin(), vec.end(), 
                       out.begin(),
                       [](double v) { 
                           return std::sqrt(std::sin(v)*std::cos(v)); 
                       }
        );
    }
}

Benchmark:

// MSVC: par and seq only
BENCHMARK_CAPTURE(BM_Trigonometry, std_seq, std::execution::seq);
BENCHMARK_CAPTURE(BM_Trigonometry, std_par, std::execution::par);
BENCHMARK_CAPTURE(BM_Trigonometry, pstl_seq, pstl::execution::seq);
BENCHMARK_CAPTURE(BM_Trigonometry, pstl_par, pstl::execution::par);

I’m running all benchmarks with the following params:

RangeMultiplier(10)->Range(1000, 1000000)->Unit(benchmark::kMicrosecond);

So that gives us execution for 1000 elements, 10k, 100k and 1000 million elements. The time is shown using microseconds.

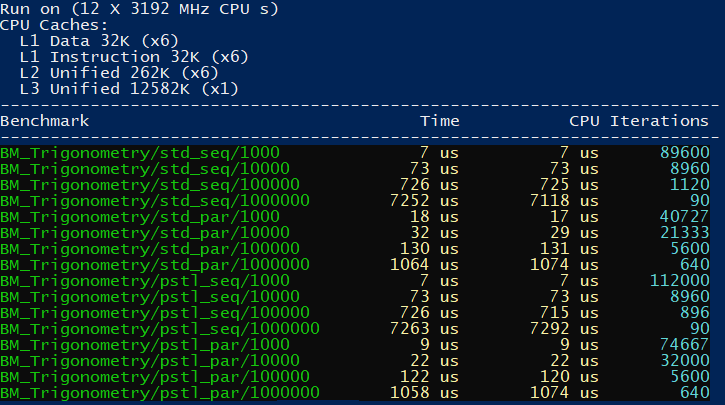
Here are the results on the MSVC Compiler, Release x64:


Google Benchmark measures the time of execution that happens in the for-loop:

for (auto _ : state)
{
    // test code...
}

It runs our code enough times (number of iterations) to provide stable statistical results. In general the faster the code, the more iteration it needs. That’s why you will see different numbers of iterations near the results.

To compare it easier, here’s a chart with the results for 100k and 1 million elements:


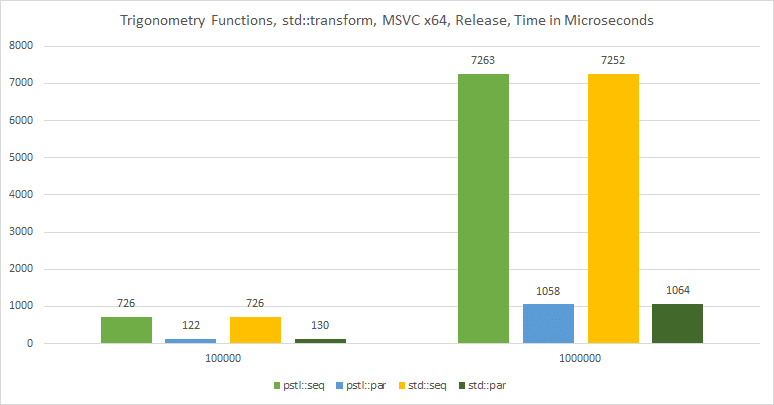
On MSVC the performance is very similar.

My machine has 6 cores, 12 threads. So parallel policies were able to achieve almost 7x speedup.

And also here are the results when compiling under Intel® C++ Compiler 18.0

The code

BENCHMARK_CAPTURE(BM_Trigonometry, pstl_seq, pstl::execution::seq);
BENCHMARK_CAPTURE(BM_Trigonometry, pstl_unseq, pstl::execution::unseq);
BENCHMARK_CAPTURE(BM_Trigonometry, pstl_par, pstl::execution::par);
BENCHMARK_CAPTURE(BM_Trigonometry, pstl_par_unseq, pstl::execution::par_unseq);

The results


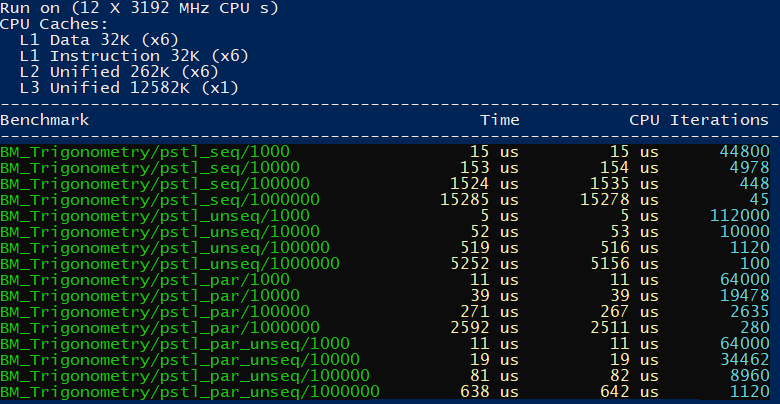
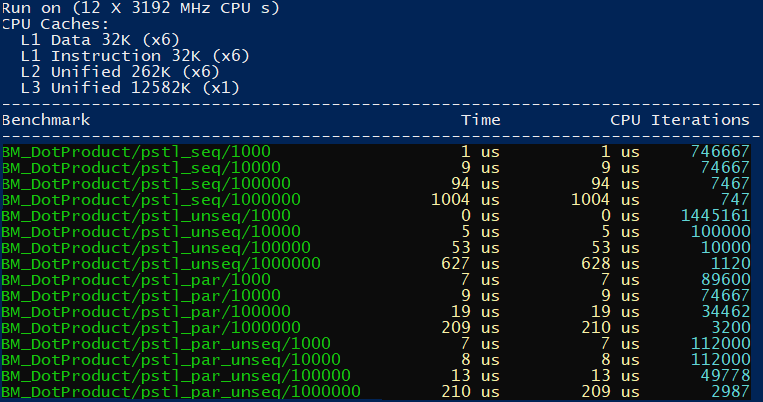
Intel® C++ Compiler 18.0 doesn’t support Standard Parallel Algorithms, so I only use pstl::execution policies. What’s interesting here is that we see a real performance improvement when using unsequenced policies.

For example, for one million elements unsequenced policy is 3x faster than the sequential version. I need to examine the results as they don’t look right. For example, the sequential version is 2x slower than the sequential version on MSVC.

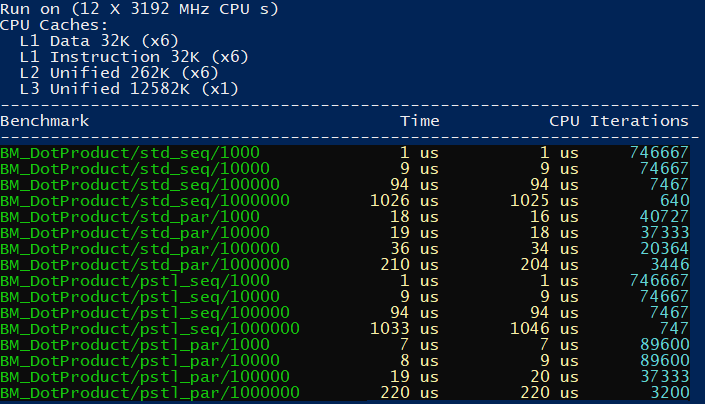
Dot Product (using transform_reduce)  

The previous tests used transform that can be easily parallelised. However, how about more complex parallel invocation?

For example, using reduce operation - which is another core component of parallel algorithms.

Reduction needs to work with several steps to compute a single result of the input range of elements. std::reduce is a form of std::accumulate.

C++ offers a fused version of two algorithms: reduce and transform. That way elements in the container are firstly transformed using some unary operation, and then the results are reduced (“summed”) into a single value.

We can use the pattern to compute the dot product of two large vectors. In the first step - transform - we’ll multiply components from the vector, and then add the results together.

A dot B = a1*b1 + ... + an*bn;

C++ code:

template <typename Policy>
static void BM_DotProduct(benchmark::State& state, Policy execution_policy)
{
    std::vector<double> firstVec(state.range(0));
    std::vector<double> secondVec(state.range(0));

    //initialize vectors with random numbers
    std::generate(pstl::execution::par, 
                  firstVec.begin(), firstVec.end(), 
                  []() { return GenRandomFloat(-1.0f, 1.0f); });
    std::generate(pstl::execution::par, 
                  secondVec.begin(), secondVec.end(), 
                  []() { return GenRandomFloat(-1.0f, 1.0f); });

    for (auto _ : state)
    {
        double res = std::transform_reduce(execution_policy,
                     firstVec.cbegin(), firstVec.cend(), 
                     secondVec.cbegin(), 0.0,
             std::plus<double>(), 
             std::multiplies<double>());
        benchmark::DoNotOptimize(res);
    }
}

Results on MSVC:


The chart:

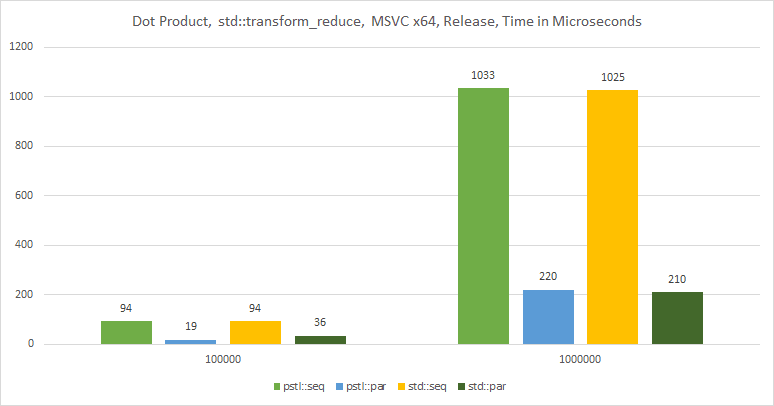
And here are the results when compiled using Intel® C++ Compiler:

Sorting  

Another more complex pattern for parallel execution is sorting.

I’ll be creating vec4 objects, and I’d like to sort them on the X-axis.

We can use the following code for the benchmark:

template <typename Policy>
static void BM_SortPoints(benchmark::State& state, Policy execution_policy)
{
    std::vector<glm::vec4> points(state.range(0), { 0.0f, 1.0f, 0.0f, 1.0f });
    std::generate(points.begin(), points.end(), []() {
        return glm::vec4(GenRandomFloat(-1.0f, 1.0f), 
                         GenRandomFloat(-1.0f, 1.0f), 
                         GenRandomFloat(-1.0f, 1.0f), 1.0f);
        }
    );

    for (auto _ : state)
    {
        std::sort(execution_policy, points.begin(), points.end(),
            [](const glm::vec4& a, const glm::vec4& b) { 
                return a.x < b.x; 
            }
        );
    }
}

The results from MSVC:


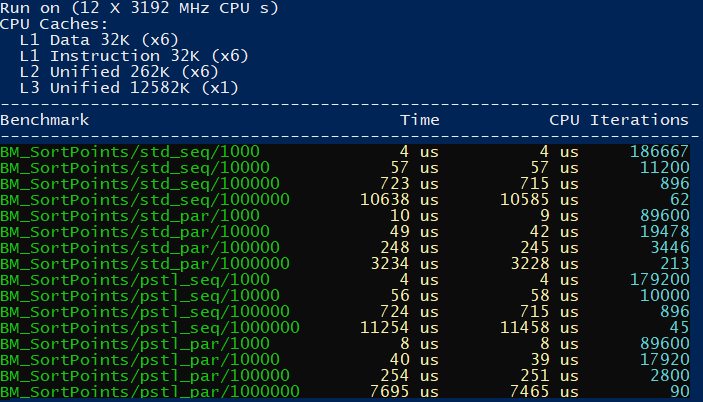
The chart:

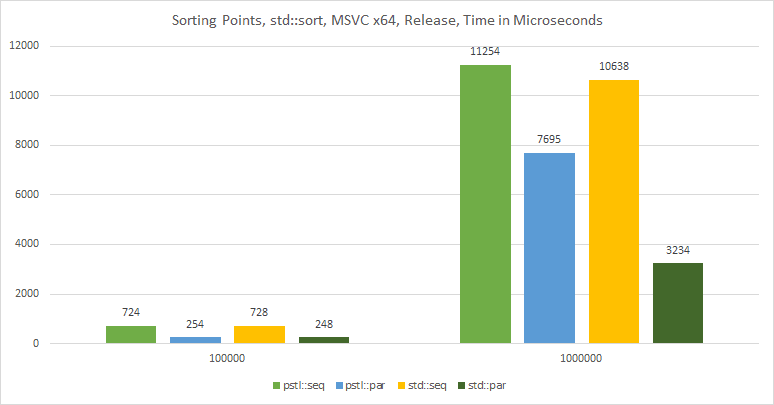
And from the Intel® C++ Compiler:


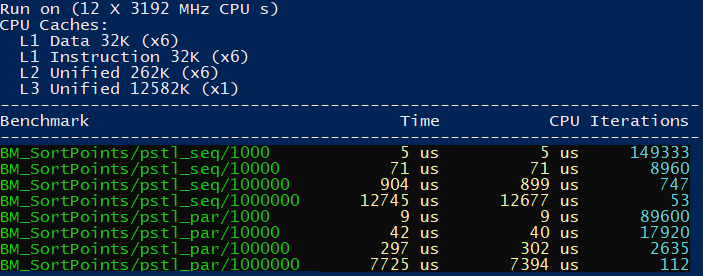
The above example shows only seq and par executions as unsequenced policies are not supported in this case.

Extra - Counting And Zip Iterators  

When I dig into the sources of Parallel STL I’ve noticed two potentially useful helpers: zip and counting iterators.

They are defined in #include <iterators.h> header file, and only reference to TBB’s iterators:

The iterators are handy when you’d like to access several containers in one parallel algorithm.

Here’s an example where I compute the profit from orders:

profit = price * (1.0f - discount)*quantity

And the code:

std::vector<double> prices(VecSize);
std::vector<unsigned int> quantities(VecSize);
std::vector<double> discounts(VecSize);

std::for_each(execution_policy, 
              pstl::counting_iterator<int64_t>(0),
              pstl::counting_iterator<int64_t>(VecSize),
    [&prices, &quantities, &discounts](int64_t i) {
        prices[i] = GenRandomFloat(0.5f, 100.0f);
        quantities[i] = GenRandomInt(1, 100);
        discounts[i] = GenRandomFloat(0.0f, 0.5f); // max 50%
    }
);

// compute profit:
std::vector<double> profit(VecSize);
std::transform(execution_policy, 
               pstl::counting_iterator<int64_t>(0), 
               pstl::counting_iterator<int64_t>(VecSize), profit.begin(),
       [&prices, &quantities, &discounts](int64_t i) {
            return (prices[i] * (1.0f - discounts[i]))*quantities[i];
       }
);

Currently, the iterators are TBB/Parallel STL specific, so they are not fully conformant with STL (missing default constructor for iterators - see issue 22 at github).

I’ve also created a benchmark for the above example:

template <typename Policy>
static void BM_CountingIter(benchmark::State& state, Policy execution_policy)
{
    const auto VecSize = state.range(0);
    std::vector<float> prices(VecSize);
    std::vector<unsigned int> quantities(VecSize);
    std::vector<float> discounts(VecSize);
    std::vector<float> profit(VecSize);

    std::for_each(execution_policy, 
                  pstl::counting_iterator<int64_t>(0), 
                  pstl::counting_iterator<int64_t>(VecSize),
                  [&prices, &quantities, &discounts](int64_t i) {
                      prices[i] = GenRandomFloat(0.5f, 100.0f);
                      quantities[i] = GenRandomInt(1, 100);
                      discounts[i] = GenRandomFloat(0.0f, 0.5f); // max 50%
                  }
    );

    for (auto _ : state)
    {
        std::transform(execution_policy, 
                       pstl::counting_iterator<int64_t>(0), 
                       pstl::counting_iterator<int64_t>(VecSize), profit.begin(),
                       [&prices, &quantities, &discounts](int i) {
                           return (prices[i] * (1.0f - discounts[i]))*quantities[i];
                       }
        );
    }
}

Here are the results when running on Intel® C++ Compiler:


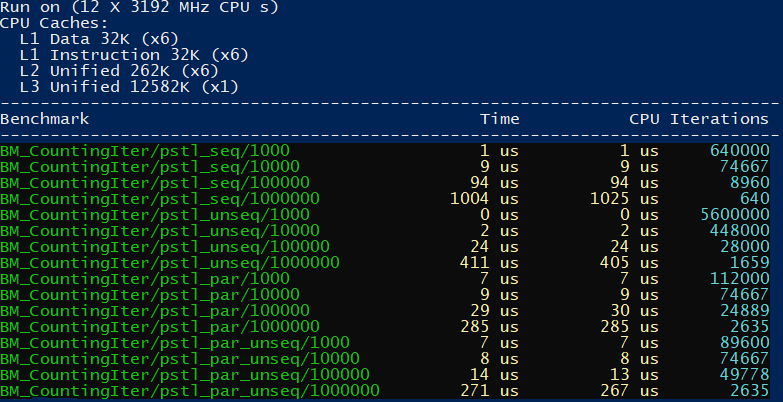
In the above test run we can see that unseq yields 2.5X speedup over the sequential version. However in par_unseq we don’t get much extra speed over the par version.

In C++20 we might have a similar counting iterator that will be implemented along with the Ranges.

Summary  

It was an interesting experiment!

In most cases on MSVC TBB implementation and internal Visual Studio’s approach performed similarly on my Windows machine.

Intel offers unsequenced policies so it would be a good option to check Parallel STL on Clang and GCC (as they support TBB and also SIMD constructs with OpenMP).

I look forward to getting the standard algorithm support on GCC and Clang.

Special thanks to one developer from Intel - Alexey Kukanov - for providing me with a feedback for the article.

Below you can see a summary of the differences between Parallel STL and Standard C++.

Your Turn & feedback  

Have you played with Intel Parallel STL or TBB?
Please try to replicate my benchmarks on your machine and show me your results.

Special Thanks to the Conan Team

I’m grateful to the Conan Team for sponsoring the article and also providing the real value - a fresh Intel Parallel STL Conan package. You can easily use it in your projects.

References